শূন্যের আবিষ্কার ও দশভিত্তিক সংখ্যা পদ্ধতির প্রচলন। গণিতের ইতিহাসে অন্যতম শ্রেষ্ঠ ঘটনাগুলোর একটি হল দশভিত্তিক সংখ্যা পদ্ধতির প্রচলন ও আরেকটি হল শূন্যের আবিষ্কার। দুটোই ভারতীয় গণিতবিদদের আবিষ্কার এ বিষয়ে কোন দ্বিমত নেই। এছাড়া ঋণাত্মক সংখ্যার ব্যবহারের সূত্রপাত এখান থেকেই।
এটা বললে ভুল হবে না যে গণিতে শূন্য ধারণার আবিষ্কার ছিল বিপ্লবী। শূন্য কিছুই নয় বা কিছুই না হওয়ার ধারণার প্রতীক। এটি একটি সাধারণ ব্যক্তির গণিতে সক্ষম হওয়ার ক্ষমতা তৈরি করে। এর আগে, গণিতবিদদের সহজ গাণিতিক গণনা করার জন্য সংগ্রাম করতে হয়েছিল। আজকাল শূন্য একটি পরিসংখ্যানগত প্রতীক এবং জটিল সমীকরণ এবং গণনার ক্ষেত্রে একটি ধারণা হিসাবে ব্যবহৃত হয়। এর সাথে শূন্যও কম্পিউটারের মূল ভিত্তি।
তারা গাণিতিকভাবে চারপাশের সবকিছুর ব্যাখ্যা দিতে চেষ্টা করতেন- একই ধরণের চেষ্টা লক্ষ্য করা যায় প্রাচীন গ্রীসের গণিতচর্চাতেও। এরকম ক’জন প্রাচীন ভারতীয় জ্যোতির্বিদ ও গণিতজ্ঞ হলেন আর্যভট্ট, ব্রহ্মগুপ্ত, ভাস্করাচার্য, বরাহমিহির, মহাবীর, লল্ল, পদ্মনাভ, শ্রীধর, নারায়ণ পন্ডিত (গণিত কৌমুদীর লেখক)।
তাদের বিভিন্ন গ্রন্থে অনেক গাণিতিক সমস্যার বর্ণনা পাওয়া যায়; পাশাপাশি সেখানে পাটীগণিত, বীজগণিত, সমতল ও গোলীয় ত্রিকোণমিতি বিষয়ক বিভিন্ন প্রক্রিয়া উদ্ভাবন ও ব্যবহারের বিবরণ পাওয়া যায়। সময়ের স্রোতে এসবের অনেক কিছুই আজ অর্থহীন মনে হতে পারে, কিন্তু এই ইতিহাসটুকুও যদি আমরা হারিয়ে ফেলি তবে বলার মত আমাদের আর কিছুই অবশিষ্ট থাকে না। এখানে সেই মহামনীষীদের শ্রদ্ধাভরে স্মরণ করছি।
মায়াসভ্যতা ছিল বর্তমান মেক্সিকো ও উত্তর ব্রাজিল অংশে। এর ব্যবহার আমরা আজও আমাদের ঘড়িতে এবং কোণ পরিমাপের ক্ষেত্রে দেখতে পাই। আর ৩০০০ বছরের পুরনো রোমান সংখ্যা ছিল দশভিত্তিক তবে শূন্যবিহীন। আজ থেকে ২২০০ বছর পূর্বে ভারতীয়রা দশভিত্তিক সংখ্যাগণনা পদ্ধতি প্রচলন করেন যেখানে শূন্যের ব্যবহার লক্ষ্য করা যায়।নবম শতাব্দীতে আরবী সংখ্যা পদ্ধতিকে আধুনিকায়ন করেন আল-খোয়ারজমি, তিনি ভারতীয় সংখ্যা পদ্ধতির অনুকরণেই এমনটি করেন।
ধারণা করা হয় ভারতীয়রা যখন দশভিত্তিক সংখ্যা পদ্ধতির প্রচলন করে তখনই তারা গণিতের রহস্যময়ী অংক ‘শূন্য’ আবিষ্কার করেন বা আরো স্পষ্টভাবে বললে বলতে হয় ‘শূন্য’ কে তারাই প্রথম গাণিতিক মর্যাদা প্রদান করেন। সেই সময় এক থেকে নবম অংকের পর দশম অংকের নাম দেওয়া হয় ‘শূন্য বিন্দু’ এবং যার প্রতীক ছিল ( . ) –একটি বিন্দু।
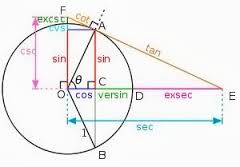
(খ্রিস্টপূর্ব ৪৭৬-৫৫০) প্রাচীন ভারতীয় গণিতবিদদের মধ্যে যার নাম সর্বাগ্রে আসে তিনি আর্যভট্ট। তিনি দু’টি গ্রন্থ রচনা করেছিলেনঃ “আর্যভট্টীয়” ও “আর্যসিদ্ধান্ত”। এখানে তিনি ত্রিকোণমিতির বিভিন্ন সূত্র ও সিদ্ধান্ত লিপিবদ্ধ করেন, যা ত্রিকোণমিতির ভিত্তিস্বরূপ। ত্রিকোণমিতিতে সাইন এবং কোসাইন এই নাম দু’টোর ব্যুৎপত্তি ঘটেছিল আর্যভট্টের দেওয়া নাম থেকেই।
কোন বর্গক্ষেত্রের কর্ণ ও বাহুর দৈর্ঘ্যের অনুপাত যেমন অমূলদ সংখ্যা তেমনি বৃত্তের পরিধি ও ব্যাসের অনুপাত যে অমূলদ হবে তাও তিনি জানতেন এবং তিনি এই অমূলদ সংখ্যার মান ধরেছিলেন ৩.১৪১৬। যা আজকের পাইয়ের মানের সাথে সঙ্গতিপূর্ণ; তাছাড়া তিনি উল্লেখ করেছিলেন যে এটি আসন্ন মান।
এই পাইয়ের মান ব্যবহার করে তিনি পৃথিবীর ব্যাসার্ধ নির্ণয় করেন, তবে ইতিপূর্বেই গ্রীক ও রোমানরা কাজটি করেছিলেন। তবে তিনিই প্রথম ব্যক্তি যে এই গ্রহের আয়তন নির্ণয় করেছিলেন। তার আরেকটি গুরুত্বপূর্ণ অবদান হল দুইটি অজানা রাশি সম্বলিত একঘাতবিশিষ্ট সমীকরণের সমাধান নির্ণয় পদ্ধতি।
তিনিই প্রথম nসংখ্যক স্বাভাবিক সংখ্যার বর্গের ও ঘনের সমষ্টি নির্ণয়ের সরল সূত্র আবিষ্কার করেন। এছাড়া তিনি শূন্যের আবশ্যকতা বর্গমূল ও ঘনমূল নির্ণয়ের সূত্রের সাহায্যে তুলে ধরেন। তার একটি স্তোত্রে পাওয়া যায় “স্থানম স্থানম দশ গুণম” কথাটি যার অর্থ স্থানে স্থানে দশ গুণ করে পরিবর্তিত হয়, এখান থেকেই স্পষ্ট বুঝা যায় তিনি দশভিত্তিক সংখ্যা পদ্ধতির কথা বলছেন। এই গ্রন্থে আর্যভট্ট জ্যোতির্বিদ্যার অনেক সিদ্ধান্তও লিপিবদ্ধ করেন।
তিনি এখানে পৃথিবীর আহ্নিক গতির কথা আলোচনা করেন এবং জ্যোতির্বিদ্যায় দিনরাত্রির গণনার জন্য ঔদায়িক ও অর্ধরাত্রিক নামে দু’টি পদ্ধতির প্রস্তাবনা করেন। ঔদায়িক পদ্ধতিতে সূর্যোদয় হতে দিন শুরু হয়, যা আজও বাংলা বর্ষরীতিতে প্রচলিত আছে; অপরদিকে অর্ধরাত্রিক পদ্ধতিতে মাঝরাত থেকে দিনের শুরু ধরা হয়, যা বর্তমানে বিশ্বজুড়ে ব্যবহৃত হচ্ছে।
এই গ্রন্থেই তিনি বলেন-“পৃথিবী গতিশীল, আকাশ নিশ্চল এবং বস্তুসমূহ কোন কিছুর টানেই নিচে পড়ে”। যদিও মহাকর্ষের কথা তিনি বলেননি তবুও নির্দ্বিধায় বলা যায় তিনি সঠিক মতবাদ দিয়েছিলেন। তিনি ব্যাখ্যা করেন দিন ও রাত হওয়ার কারণ এবং একই সাথে সাত দিনে সপ্তাহ ও সপ্তাহের সাতটি দিনের নামও তিনি ঠিক করেন।
তিনি মনে করতেন পৃথিবী বৃত্তাকার নয় বরং উপবৃত্তাকার পথে আবর্তনশীল। তিনি এখানে উল্লেখ করেন যে চাঁদের আলো আসলে সূর্যের প্রতিফলিত আলো। সূর্যগ্রহণ ও চন্দ্রগ্রহণের বিজ্ঞানসম্মত ব্যাখ্যাও তিনি প্রদান করেন। এছাড়া তিনি সূর্যগ্রহণ ও চন্দ্রগ্রহণের সময় ও ব্যাপ্তি নির্ধারণের জন্য একটি গাণিতিক পদ্ধতির প্রবর্তন করেন।
১৭৬৫ সালের ৩০ আগস্ট একটি চন্দ্রগ্রহণ হয়েছিল সেদিন পরীক্ষা করে দেখা যায় ১৭৫২ সালে Guillaume Le Gentile কর্তৃক প্রবর্তিত চার্ট এর চেয়ে ২২০০ বছর পূর্বের আর্যভট্টের গণনা বেশি কার্যকর। তিনি দিনের দৈর্ঘ্য নির্ণয় করেন ২৩ ঘন্টা ৫৬ মিনিট ৪.১ সেকেন্ড যেটি বর্তমানে ২৩ ঘন্টা ৫৬ মিনিট ৪.০৯১ সেকেন্ড। তার আবিষ্কৃত বিভিন্ন সূত্র ধরেই পরবর্তীকালের গণিতবিদেরা অগ্রসর হয়েছিলেন। তার প্রমাণ মেলে আল-খোয়ারিজমি ও আল-বিরুনিসহ অনেক গণিতবিদের রচনায়। সকল ভারী বস্তুই পৃথিবীর কেন্দ্রের দিকে আকৃষ্ট হয়।

ব্রহ্মগুপ্তঃ
জ্যামিতিতে ব্রহ্মগুপ্তের অবদান অনেক। তিনি বৃত্তস্থ চতুর্ভুজের বাহুসমূহের দৈর্ঘ্যের সাহায্যে ঐ চতুর্ভুজের কর্ণের দৈর্ঘ্য পরিমাপের নিয়ম আবিষ্কার করেন, যা জ্যামিতির ইতিহাসে অত্যন্ত গুরুত্বপূর্ণ। তার রচিত “খন্ড-খাদ্য” গ্রন্থে তিনি ত্রিভুজের ক্ষেত্রফল ও এর পরিব্যাসার্ধ নির্ণয়ের সূত্র প্রদান করেন। যা থেকে আমাদের অতি
পরিচিত ত্রিভুজের ‘সাইন সূত্র’টি পাওয়া যায়।
এছাড়া তার প্রমাণ করা একটি উপপাদ্য আমাদের নবম শ্রেণির পাঠ্যবইয়ে আছে। এছাড়া উচ্চতর গণিতের সন্নিবেশ ও প্রক্ষেপণ তত্ত্বের জনক হিসেবে তিনি স্মরণীয় হয়ে থাকবেন। তিনি এই প্রক্ষেপণ তত্ত্ব ব্যবহার করে আর্যভট্ট প্রণীত সাইন সারণী আরো ক্ষুদ্র মানের জন্য প্রস্তুত করেন। বর্তমানে এই প্রক্ষেপণ তত্ত্ব ‘নিউটন স্টারলিং ইন্টারপোলেশন’ (Newton Starling Interpolation) নামে পরিচিত।
অনন্ত শ্রীভগবানের মধ্যে অসংখ্য জীবের জন্ম ও ধ্বংস হচ্ছে কিন্তু তাতে তার কোন পরিবর্তিন হয় না। তেমনি অনন্ত বা অসীমের সাথে কোন কিছু যোগ বা বিয়োগ করলে তারও কোন পরিবর্তন হয় না।
ভাস্করাচার্যঃ
প্রাচীন ভারতের সবচেয়ে পরিচিত ও আলোচিত গণিত বিষয়ক গ্রন্থ “লীলাবতী”-র লেখক ভাস্করাচার্য। তিনি দ্বাদশ শতাব্দীতে “সিদ্ধান্ত-শিরোমনি” নামে একটি গ্রন্থ রচনা করেন যার প্রথম অংশ “লীলাবতী”। লীলাবতীতে তিনি পাটিগণিতের বিভিন্ন সমস্যা এবং এর সমাধানের নিয়ম উল্লেখ করেন। “সিদ্ধান্ত-শিরোমনি”-র পরবর্তী তিনটি খন্ডে তিনি বীজগণিত ও জ্যোতির্বিদ্যা সম্পর্কে আলোচনা করেন।
ভাস্করাচার্যের সময়ে ভারতবর্ষে গণিতচর্চার অন্তিম সময় ঘনিয়ে আসে এবং এ সময় ভারতবর্ষ মুসলিম শাসকদের অধীনে চলে যায়। মুসলমান শাসকদের কল্যাণে ভারতীয় জ্ঞান-বিজ্ঞান বহির্জগতে প্রবেশের পথ খুঁজে পায়। আরবরা এ সময় ভারতীয় গ্রন্থ অনুবাদ করেন; এরকম কয়েকটি হলঃ সিন্দহিন্দ (ব্রহ্মস্ফুটসিদ্ধান্ত), আরকন্দ (খন্ডখাদ্যক), আল আরজাওয়াদ (আর্যভট্টীয়)।
আরব গণিতবিদদের হাত ধরে এসব গ্রন্থ রোমানদের হাতে যায়; এবং রোমানদের মাধ্যমে ইউরোপের গণিতশাস্ত্র আধুনিক রূপ লাভ করে। তাই বলা যায় আধুনিক গণিতের পটভূমিতে ভারতীয় গণিতবিদদের গৌরবময় কৃতিত্ব রয়েছে। আর আধুনিক গণিত শাস্ত্রের যুগান্তকারী প্রতিভা নিয়ে জন্ম গ্রহন করেছিলেন রামানুজন। রামানুজনকে বলা হয় গণিতবিদদের গণিতবিদ।
এখানে আমি যা কিছু লিখেছি তার কোন কিছুই নতুন নয়; এমনকি আমি বিভিন্ন বই থেকে আংশিক বা পুরোপুরি টুকলিফাই করেছি; যারা এই নকলকৃত অংশগুলো শনাক্ত করে বৃত্তকে বর্গক্ষেত্রে রুপান্তর করার
আনন্দ লাভ করতে চান, তাদের জন্য সহায়ক হবে নিচের তালিকাটিঃ
লেখক- আতাউর রহমান-ময়মনসিংহ-বাংলাদেশ।
তথ্যসূত্রঃ-
- অগ্নিকুণ্ড মহাদেব মন্দির : বাংলাদেশে শিব মন্দিরের অগ্নিশিখা, যা কখনই নিভে যায় না, অমীমাংসিত ধাঁধা।
- দেশভাগ: যখন ভারত ধর্মের ভিত্তিতে বিভক্ত হয়েছিল, তখন হিন্দু সংখ্যাগরিষ্ঠ সিন্ধু কেন ভারত থেকে পৃথক হয়েছিল।
- আফগানিস্তানের ইতিহাস: আফগানিস্তানের ইতিহাসের ১৩ আশ্চর্যজনক তথ্য যা, জানলে আপনি অবাক হয়ে যাবেন।
- মুসলিম মেয়েরা কি হিন্দু ধর্মে দীক্ষিত হওয়ার পর অনুশোচনা করে যেমন অনেক হিন্দু মেয়েরা আফসোস করে এবং ভালোবাসার জন্য ইসলাম গ্রহণ করার পর কষ্ট পায়?
- হিন্দু ধর্ম কি গ্রহণ করা যায়, হিন্দু ধর্ম গ্রহন করার নিয়ম কি ?




