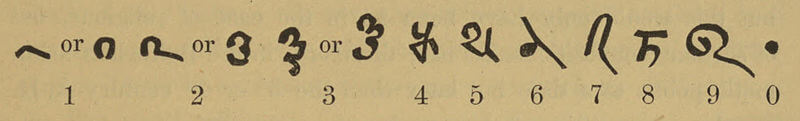গণিতবিদ্যায় আমাদের আবদান……………………………………….।।।

প্রাচীন
ভারতীয় গণিতবিদ্যা নিয়ে আমি বিভিন্ন পেশার লোকজনের সঙ্গে আলোচনা করেছি।
সেই আলোচনায় প্রায়শই ‘বৈদিক গণিতবিদ্যা’র ’১৬ সুত্রের’ কথা উঠে এসেছে।
অনেকেই মনে করেন যে গণনার ক্ষেত্রে প্রাচীন এই সূত্রগুলি আমাদের এক
ঐন্দ্রজালিক ক্ষমতা বা ম্যাজিকাল পাওয়ার প্রদান করে। বাস্তব কিন্তু
সম্পূর্ণ আলাদা। এই ‘বৈদিক গণিতবিদ্যা’ আসলে বৈদিক যুগের নয়, এগুলি
সন্দেহাতীতভাবে বিংশ শতাব্দীর আবিষ্কার। ‘ষোড়শ সূত্র’ প্রকৃতপক্ষে
প্রবর্তন করেন ভারতী কৃষ্ণ তীর্থজী, যিনি ১৯২৫ সাল থেকে আমৃত্যু (১৯৬০ সাল
পর্যন্ত) পুরীর শঙ্করাচার্য  ছিলেন। এর সঙ্গে তিনি আরও কিছু পাটিগণিত ও
বীজগণিতের নিয়ম প্রণালীও প্রবর্তন করেন। অতএব, এইসব ‘সূত্র’ বা গণিতের
নিয়ম প্রণালীর সঙ্গে বেদ বা বেদ পরবর্তী ভারতবর্ষের গাণিতিক ঐতিহ্যের কোন
যোগাযোগ নেই। বৈদিক গণিতের নামে শিশুদের যা শেখানো হয় তার মাধ্যমে প্রাচীন
ঋষিদের অতি-প্রাকৃত ব্যক্তিত্বকেই
তুলে ধরার চেষ্টা করা হয়। এই ‘বৈদিক গণিত’ সম্পূর্ণভাবে কিছু
শব্দবন্ধের
ওপর ভিত্তি করে গড়ে উঠেছে, আধুনিক সংস্কৃত শৈলীতে যা ‘সূত্র’ নামে পরিচিত।
এর কোন বিশ্বাসযোগ্যতা আছে বলে মনে হয়না। অথচ, বৈদিক গণিত নিয়ে এই হইচইকে একটা রসিকতা বলেও আর উড়িয়ে দেওয়া যাচ্ছে না। বর্তমানকালে যে ধরনের বাতাবরণে এই হইচই সফল
হচ্ছে তার মূলে প্রাচীনকালের জ্ঞান সম্পর্কে আমাদের অজ্ঞতা অন্যতম। এটা
খুবই দুঃখের ব্যাপার যে দীর্ঘ ৩০০০ বছরের প্রয়াস ও গণিততত্ত্বের সাধনার
ঐতিহ্যকে জনসাধারণের এক বড় অংশ বুঝেছে খুবই সাধারণ দৃষ্টিভঙ্গি থেকে। এর অনেকটা মনগড়াও বটে। এই দৃষ্টিভঙ্গি গণিতবিদ্যার প্রতি আমাদের এক চরম উদাসীনতার পরিচায়ক।

প্রাচীন ভারতের সাফল্য সম্পর্কে যে আমাদের প্রচণ্ড অবহেলা জড়িত, তা কিন্তু নয়। বরঞ্চ উলটোটাই
সত্যি। অনেক জনপ্রিয় ও তথ্যপূর্ণ রচনা পাওয়া যাবে যেখানে অযৌক্তিকভাবে
আমাদের পূর্বপুরুষদের অপরিসীম জ্ঞানের কথাই দাবি করা হয়েছে। অথচ, পরিশীলিত
দৃষ্টিকোণ
থেকে প্রাচীন ভারতের জ্ঞান বা সাফল্যকে আমরা খুব কম ক্ষেত্রেই
বাস্তবসম্মতভাবে অনুধাবন বা উপলব্ধি করতে পেরেছি। ঔপনিবেশিক যুগে কিছু
পশ্চিমী শিক্ষাবিদের পক্ষপাতিত্বের উত্তর দেওয়ার জন্য প্রাচীন ভারতের
কৃতিত্ব নিয়ে অনেক প্রবন্ধ রচনা করা হয়েছিল । সেই সময়ে প্রতিকূল
প্রচারণার বিরুদ্ধে রুখে দাঁড়ানোর তাগিদ ছিল প্রবল। কিন্তু এই প্রতিকূলতার
বিরুদ্ধে দাঁড়ানোর জন্য প্রাচীন ভারতীয় শিক্ষার যে গভীরে যাওয়ার
প্রয়োজন ছিল তা সহজলভ্য ছিল না। তাই প্রায়শই সহজ পন্থা অনুসরণ
করা হয়েছে, যেখানে তথ্যের থেকে বক্তৃতার প্রগল্‌ভতাই প্রাধান্য পেয়েছে।
যাইহোক, সেই সময় সুধাকর দ্বিবেদীর মতো কিছু ভারতীয় শিক্ষাবিদও ছিলেন,
যাঁরা জ্ঞানমূলক দৃষ্টিভঙ্গিকে আশ্রয় করেছিলেন। যদিও তাঁদের সংখ্যা খুবই নগণ্য। এখন আমরা ঔপনিবেশিক যুগকে অনেকটা পেছনে ফেলে এসেছি। সারা পৃথিবী ভারতের সাফল্যকে যথেষ্ট কৌতূহল ও গুরুত্বের সঙ্গে বিবেচনা করছে। তাও, আমাদের দুর্ভাগ্য যে, পুরানো চিন্তাভাবনার আলোচনা ও নিবন্ধ এখনো অব্যাহত রয়েছে। আমার মনে হয়, এখন সময় হয়েছে সার্বভৌম এবং বুদ্ধিগতভাবে স্বনির্ভর সমাজের মানানসই পথ অবলম্বন করার। ‘তাঁরা
কি বলেছিলেন’ আর কেমনভাবে ‘আমরা আমাদের জাহির করব’ – চিন্তাভাবনার এই
পরিকাঠামো থেকে বেরিয়ে এসে উদ্দেশ্যপূর্ণ অধ্যয়ন এবং সমালোচনামূলক
মূল্যায়নের ওপর জোর দেওয়ার এটাই উপযুক্ত সময় ।

প্রকৃতপক্ষে,
পৃথিবীর গণিতবিদ্যার ঐতিহ্যে প্রাচীন ভারতের অবদান যথেষ্ট তাৎপর্যপূর্ণ।
গত ৩০০০ বছর ধরে ধারাবাহিকভাবে গণিতবিদ্যার যে অগ্রগতি ঘটেছে, বহু অংশে
আমাদের দেশ তার সাক্ষী থেকেছে। বাকি বিশ্বের সামনে অনেক গুরুত্বপূর্ণ
তত্ত্ব তুলে ধরেছে। যদিও সময়ের সঙ্গে সঙ্গে পিছিয়ে পড়েছি আমরা, বিশেষত
সাম্প্রতিক শতাব্দীগুলোতে। এই প্রবন্ধে এমনই কিছু বুদ্ধিগত প্রচেষ্টার আকর্ষণীয় ইতিহাস তুলে ধরা হয়েছে যা প্রাচীন ভারতের সমৃদ্ধ গণিতবিদ্যার পরিকাঠামো গঠন করেছিল।

ভারতবর্ষে গণিতবিদ্যা চর্চার যে ঐতিহ্য তা বুঝতে গেলে অন্ততপক্ষে আমাদের বেদের যুগে ফিরে যেতে হবে। বেদের সূত্রগুলোতে রয়েছে আধ্যাত্মিক
থেকে বৈষয়িক, জীবনের নানা ক্ষেত্রে প্রযোজ্য আলোচনা। বিষয়বস্তুর এই
বৈচিত্র ও ব্যাপ্তি সত্ত্বেও যেটা সহজে নজরে আসে তা হল বড় সংখ্যার প্রতি
বিশেষ আকর্ষণ। যেহেতু সেযুগে শিক্ষার প্রসার মূলত ঘটেছিল মৌখিকভাবে, তাই
সংখ্যার লিখিতরূপ ছিল না। কিন্তু সংখ্যাগুলো বর্ণনা করতে গিয়ে ১০ এর
বিভিন্ন ঘাত (combination of powers of 10) ব্যবহৃত হয়েছে। তাই এটা ভাবা
যুক্তিযুক্ত হবে যে, পরে যখন লিখিত সংখ্যার ক্ষেত্রে দশমিক পদ্ধতির প্রচলন শুরু হল, তার অনেকটাই পুরানো বৈদিক সূত্রের এই ধারা অনুসরণ করে এসেছিল।

খ্রিস্ট
পরবর্তী শতাব্দীর একেবারে শুরুর দিকে ভারতবর্ষে ‘0’ এর ব্যবহারের সঙ্গে
দশমিক পদ্ধতির প্রচলন হয়েছিল। পারস্য আর আরবের মাধ্যমে তা ছড়িয়ে পড়েছিল
পশ্চিমের দেশগুলিতে। যদিও এর আগেই দশমিক পদ্ধতির বেশ কিছু অংশের ব্যবহারের
উল্লেখ পাওয়া যায় ব্যাবিলনীয়, চীনা, মায়ার মতো প্রাচীন সভ্যতাতে।
দশমিক পদ্ধতির সাহায্যে স্বাভাবিক সংখ্যার (Natural number) প্রকাশ
(representation) কালক্রমে বিবর্তিত হয়ে তার বর্তমান বহুল প্রচলিত রূপ
পেয়েছে। ষোড়শ শতাব্দীতে ইউরোপে
ভগ্নাংশের ব্যবহার সংখ্যাতত্ত্বের একটি অন্যতম অংশ হয়ে উঠেছিল, যদিও এর
মধ্যে আরবকে জড়িয়ে কিছু মধ্যবর্তী ইতিহাস আছে। সংখ্যাতত্ত্বের অগ্রগতি
গণিতবিদ্যার উন্নতির ক্ষেত্রে অন্যতম প্রধান ধাপ এবং সার্বিকভাবে বিজ্ঞান ও
প্রযুক্তিবিদ্যার অগ্রগতির ক্ষেত্রে এর অবদান অনস্বীকার্য। সংখ্যাতত্ত্বের
এই ক্রমবিবর্তনের ইতিহাস থেকে শিক্ষা পাওয়া যায় যে কোনো মতবাদ বা
ধারণার (Idea) অগ্রগতির পিছনে রয়েছে বহু যুগে বহু মানুষের অবদান। এটি একটি
সর্বব্যাপী (inclusive) ঘটনা। এই অগ্রগতিতে যাঁরা অবদান রেখেছেন তাদের
সাথে আমাদের যোগসূত্র আছে বলে আনন্দ ও গর্ব হওয়া উচিত। কিন্তু, সেই সাথে
অন্যদের ভূমিকাও উপলব্ধি করা দরকার।

এটা
সর্বজনবিদিত যে বৈদিক যুগে যজ্ঞের বেদী নির্মাণের অনুষঙ্গে জ্যামিতির
চর্চা হত। ‘শুল্ব সূত্রে’ (Sulvasutra) বেদী নির্মাণের বিস্তারিত বিবরণ
আছে। এখানে বিভিন্ন জ্যামিতিক তত্ত্বের ওপরও আলোকপাত করা আছে। এইগুলি রচিত
হয়েছিল খ্রিস্টের জন্মের প্রায় এক হাজার বছর আগে। সবচেয়ে প্রথমে রচিত
হয়েছিল ‘বৌধায়ন শুল্ব সূত্র’ (Baudhayana Sulvasutra), খ্রিস্টপূর্ব আট শতাব্দীতে। এর কিছু পরেই ‘ইউক্লিডিয়ান (Euclidean) জ্যামিতি’ গ্রীকদের দ্বারা প্রণীত
হয় খ্রিস্টপূর্ব সপ্তম শতাব্দীতে। ইউক্লিডিয়ান জ্যামিতির মত এতটা এগোতে
না পারলেও ‘শুল্ব সূত্র জ্যামিতি’ ভারতবর্ষে জ্যামিতির অগ্রগতির ক্ষেত্রে
একটা গুরুত্বপূর্ণ অধ্যায় ছিল। অনেক বিষয়ের মধ্যে এই শুল্ব
সূত্রের জ্যামিতিবিদরা পরিচিত ছিলেন ‘পীথাগোরাসের সূত্র’-এর সাথে –
পীথাগোরাসের জন্মের দুশো বছরেরও আগে! প্রধান চারটি শুল্ব সূত্রের
প্রতিটাতেই ‘পীথাগোরাসের সূত্র’-এর স্পষ্ট বর্ণনা আছে। এই জ্যামিতিবিদরা
তাঁদের তৈরি জ্যামিতির কাঠামোর মধ্যেই আলোচনা করেছিলেন কীভাবে একটি
বর্গক্ষেত্রের সমান ক্ষেত্রফল বিশিষ্ট বৃত্ত অঙ্কন করা যায়, বা এর
উলটোটাও। ২-এর বর্গমূলের আসন্নমান নির্ণয়ের কাজও তাঁরা যথেষ্ট ভালভাবে করেছিলেন।

যদিও
এটা সাধারণত স্বীকৃত হয়না, শুল্ব সূত্র জ্যামিতির নিজেরই বিবর্তন হচ্ছিল।
এখনো বেঁচে থাকা চারটি মুখ্য সূত্রের উপাদানের পার্থক্য থেকে এটা দেখা
যায়। কিছু সংশোধন বিশেষভাবে লক্ষণীয়। উদাহরণ হিসাবে বলা যেতে পারে,
অন্যান্য প্রাচীন সংস্কৃতির মতো শুল্ব সূত্রের প্রথম যুগে মনে করা হত
বৃত্তের পরিধি ও ব্যাসের অনুপাত হল ৩, যেটা বৌধায়ন সূত্রে
(Baudhayanasutra) দেখা গেছে। কিন্তু মানব (Manava) সূত্রে একটি নতুন মান
প্রস্তাবিত হয়, যা ৩ পূর্ণ ১/৫ এর সমান। মজার বিষয় হল, এই সূত্রটি শেষ
হচ্ছে একটা বিজয়বার্তা দিয়ে যে এই নতুন মান সমস্যাটির চুলচেরা বিশ্লেষণ
করেছে। যদিও এই নতুন প্রস্তাবিত মানটিও সঠিক নয়, কিন্তু সূত্রগুলির মধ্যে
যে অগ্রগতি ঘটছিল, এটি তার সন্তোষজনক উদাহরণ হিসাবে বিবেচনা করা যেতে পারে।
বৌধায়ন সূত্রে একটি বর্গক্ষেত্রের সমান ক্ষেত্রফল বিশিষ্ট বৃত্ত খুঁজে
বের করার জন্য যে পদ্ধতির উল্লেখ করা হয়েছে, ‘মানব শুল্ব সূত্র’  (Manava
Sulvasutra)-র বিবরণে সেই পদ্ধতিরও উন্নতিসাধন হয়েছে।

আমাদের
দেশের গণিতবিদ্যার অগ্রগতির ইতিহাসে জৈন মতবাদও অত্যন্ত গুরুত্বপূর্ণ।
বৈদিক পণ্ডিতদের মতো জৈনদের গণিতবিদ্যা অধ্যয়নের প্রেরনা ধর্মীয়
ক্রিয়াকর্ম পালন থেকে আসেনি, কারণ ধর্মীয় আচার আচরণের প্রতি জৈনদের তীব্র
বিতৃষ্ণা ছিল। তাঁদের প্রেরণা
ছিল বিশ্বজগৎ সম্পর্কে গভীর অনুশীলন। জৈনরা বিস্তৃতভাবে মহাবিশ্বের
মানচিত্র রচনা করেছিলেন যেখানে গণিতবিদ্যা অঙ্গাঙ্গীভাবে জড়িয়ে ছিল।
এমনকি জৈন দর্শনেও অনেক ক্ষেত্রে গাণিতিক আলোচনার প্রতিফলন দেখা যায়।
জৈনদের প্রথম দিকের গবেষণার মধ্যে (খ্রিস্টপূর্ব পঞ্চম শতাব্দী থেকে
খ্রিস্টীয় দ্বিতীয় শতাব্দী) বিশেষভাবে উল্লেখযোগ্য হল বৃত্তের জ্যামিতি,
১০-এর বড় ঘাতযুক্ত সংখ্যার (numbers with large powers of 10) পাটীগণিত,
বিন্যাস ও সমন্বয় (permutations and combinations) এবং অসীমের (Infinity)
শ্রেণীবদ্ধকরণ (অসীম যে অনেকরকম হতে পারে সেটা তাঁরা বুঝতে পেরেছিলেন)।

খ্রিস্টপূর্ব
প্রথম সহস্রাব্দের মাঝামাঝি সময়ে শুল্ব সূত্রের মতোই জৈনরাও বুঝতে
পারেন যে বৃত্তের পরিধি ও ব্যাসের অনুপাত ৩ নয়। খ্রিস্টপূর্ব চতুর্থ
শতাব্দীতে রচিত একটি জৈন রচনা ‘সূর্যপ্রজ্ঞাপ্তি’তে (Suryaprajnapti)
রচয়িতা এই অনুপাতের প্রথাগত মান ‘৩’ কে সংশোধন করে নতুন মান হিসাবে ‘১০ এর
বর্গমূল’ কে প্রস্তাবিত করেন, যা প্রকৃত মানের অনেকটাই কাছাকাছি। বৃত্তের
পরিধি ও ব্যাসের অনুপাতের এই মান দীর্ঘদিন ধরে ভারতবর্ষে যথেষ্ট প্রভাবশালী
ছিল এবং প্রায়শই ‘জৈন মান’ হিসাবে উল্লেখ করা হত। আর্যভট এই অনুপাতের
সুপরিচিত মান ‘৩.১৪১৬’ প্রবর্তন করার পরেও অনেকদিন পর্যন্ত এই ‘জৈন মান’
ব্যবহৃত হয়েছে।
বৃত্তচাপকে (circular arc) তার অনুরূপ জ্যা (chord) ও তার উচ্চতা (height
over the chord) দিয়ে প্রকাশ করার সূত্র এবং একটি বৃত্তচাপ ও তার দুটি
জ্যা দ্বারা পরিবেষ্টিত অঞ্চলের ক্ষেত্রফল বের করার সূত্রের মতো কিছু অনন্য
সূত্রও জৈন রচনাবলীতে পাওয়া যায়। যদিও কলনবিদ্যার (Calculus) আবির্ভাবের
পরেই এই সমস্ত রাশির সঠিক মান নির্ণয়ের পদ্ধতি পাওয়া গেছে, কিন্তু
প্রাচীন জৈন পণ্ডিতরা কি ভাবে এই সমস্ত সূত্রের কথা বলেছেন যা আসন্ন মানের
খুব কাছাকাছি সেটা এখনো গবেষণার বিষয়।

কিছু
শতাব্দী স্তিমিত থাকার পর, প্রথম সহস্রাব্দের প্রথমাংশে সুস্পষ্ট গাণিতিক
কার্যকলাপ জৈন সংস্কৃতিতে আবার দেখা যায় অষ্টম শতাব্দী থেকে চতুর্দশ
শতাব্দীর মাঝামাঝি পর্যন্ত। ৮৫০ খ্রিস্টাব্দে মহাবীরের লেখা
‘গণিতসারসংগ্রহ’ অন্যতম সুপরিচিত এবং প্রভাবশালী রচনা। বীরসেনা (৮ম
শতাব্দী), শ্রীধর (৮৫০-৯৫০ খ্রিস্টাব্দ), নেমিচন্দ্র (৯৮০ খ্রিস্টাব্দের
আশেপাশে), থাক্কুরা ফেরু (১৪শ শতাব্দী) প্রমুখের নামও উল্লেখ করা যেতে
পারে। ত্রয়োদশ ও চতুর্দশ শতাব্দীতে ইসলামীয় সভ্যতা ও স্থাপত্য
(architecture) ভারতে শিকড় গাড়তে শুরু করে। থাক্কুরা ফেরু, যিনি দিল্লীর
খিলজি সুলতানের দরবারের একজন কোষাধ্যক্ষ ছিলেন, তাঁর রচিত
‘গণিতসারকৌমুদী’তে স্থানীয় জৈন সংস্কৃতির সঙ্গে ইন্দো-পারসিয়ান
সাহিত্যের সংমিশ্রণ লক্ষ্য করা যায়। এমনকি বাসস্থান নির্মাণের জন্য
গম্বুজ, খিলান বা তাঁবুর মতো যে বিভিন্ন ধরনের গাঁথনি তৈরি হতো সেগুলির
ক্ষেত্রফল ও আয়তন গণনার ক্ষেত্রেও এই সংমিশ্রণ দেখা যায়।

গাণিতিক
জ্যোর্তিবিদ্যা অথবা ‘সিদ্ধান্ত’র ধারাগুলি ভারতীয় গণিতের প্রভাবশালী এবং
কালজয়ী ঐতিহ্য। সাত শতক ধরে চলতে থাকা এই নিরন্তর উন্নয়ন ভারতীয়
বিজ্ঞানসম্মত জ্যোর্তিবিদ্যার জনক হিসাবে পরিচিত আর্যভট (৪৭৬-৫৫০ খ্রিঃ)
থেকে দ্বিতীয় ভাস্কর (১১৪-১১৮৫ খ্রিঃ), এবং তাঁরও পরে আরও অনেকের অবদানের
ফসল। এই ঐতিহ্যের ধারাবাহিকতা দেখা যায় আর্যভটের পরে অনেক শতাব্দী
ধরে বিশিষ্ট সব নামের দীর্ঘ তালিকায় : ষষ্ঠ শতকে বরাহমিহির, সপ্তম শতকে
প্রথম ভাস্কর ও ব্রহ্মগুপ্ত, নবম শতকে গোবিন্দগোস্বামী ও শঙ্করনারায়ণ, দশম
শতকে দ্বিতীয় আর্যভট ও বিজয়ানন্দী, একাদশ শতকে শ্রীপতি, দ্বাদশ শতকে
ব্রহ্মদেব ও দ্বিতীয় ভাস্কর, এবং চতুর্দশ ও ষোড়শ শতকে যথাক্রমে নারায়ণ
পণ্ডিত ও গণেশ।

এই
ঐতিহ্য, এমনকী পরবর্তীকালে কেরালার মাধব ঘরানার গবেষণার (যা আমি
পরবর্তীকালে আলোচনা করব) পিছনেও মূল গ্রন্থ হল ৪৯৯ সালে লেখা ‘আর্যভটীয়’।
এটিতে ১২১ টি চরণ (verse) চারটি অধ্যায়ে বিভক্ত যথা, গীতিকাপদ, গণিতপদ,
কালক্রিয়াপদ ও গোলপদ। প্রথম অধ্যায়, যা সৃষ্টিতত্ত্বের (cosmology)
আলোচনা করে, যেখানে একটি শ্লোক পাওয়া যায় যা বৃত্ত চাপের ২২৫ মিনিট
ব্যবধানে ২৪ টি জ্যা পার্থক্যের ছক/তালিকা বর্ণনা
করে। দ্বিতীয় অধ্যায় (গণিতপদ), নামের সাথে প্রত্যাশিতভাবেই সম্পূর্ণ
গাণিতিক বিষয়ে নিবদ্ধ যেখানে বর্গমূল ও ঘনমূল, পাই (π) -এর (৩.১৪১৬ দশমিক
মান পর্যন্ত) আসন্ন মান, বিভিন্ন জ্যামিতিক আকারের ক্ষেত্রফল ও আয়তনের
সূত্র, পরপর পূর্ণসংখ্যা ক্রমের যোগফলের সূত্র, বর্গফলের যোগ, ঘনফলের যোগ,
এবং সুদের হিসাব প্রভৃতি নির্ধারণের নিয়ম বিষয়ে আলোচনা আছে। অবশিষ্ট দুই
অধ্যায়ে আলোচ্য বিষয় জ্যোর্তিবিদ্যা, গ্রহগুলির দূরত্ব ও পারস্পরিক গতি,
গ্রহণ ইত্যাদি।

ব্রহ্মগুপ্তের
লেখা ‘ব্রহ্মস্ফুট সিদ্ধান্ত’ (ব্রহ্মর সংশোধিত নীতিমালা) একটি বিশাল বই,
বিশেষত সেই সময়ের বইগুলোর তুলনায়। এটি সিদ্ধান্ত জ্যোর্তিবিদ্যার উপর,
এবং দ্বাদশ ও অষ্টাদশ এই দুটি অধ্যায়ে ছিল বিভিন্ন গাণিতিক বিষয়। একাদশ
অধ্যায়টিতে ‘আর্যভটীয়’ সহ পূর্ববর্তী কাজের সমালোচনা করা হয়েছে।
অন্যান্য সুস্থ বিজ্ঞানী সম্প্রদায়ের মতই এইসময়ের গাণিতিক গবেষণার
ঐতিহ্যেও একাধিক, কখনও বা তিক্ত, বিতর্ক লক্ষ্য করা যায়। দ্বাদশ অধ্যায়
ঋণাত্মক সংখ্যা সহ পাটিগণিতের নিয়মগুলির শৃঙ্খলাবদ্ধ ব্যবহারের জন্য
পরিচিত। দ্বিতীয় সহস্রাব্দের মাঝামাঝি পর্যন্ত ঋণাত্মক সংখ্যার ধারণা
ইউরোপের কাছে পরিষ্কার ছিল না। এই অধ্যায়টিতে জ্যামিতি সহ তাঁর বিখ্যাত
বৃত্তীয় চতুর্ভুজের^১ (cyclic quadrilateral) ক্ষেত্রফলের
সূত্রের বর্ণনা আছে ( দুর্ভাগ্যবশত পরের কয়েকশো বছরে এই বিষয়ের উপর যাঁরা
গবেষণা করেছিলেন তাঁরা এই সূত্রের আলোচনায় “বৃত্তীয় শর্ত”-এর গুরুত্ব
বুঝতে পারেননি, যা পরবর্তীকালে গণিতজ্ঞদের কাছে সমালোচিত হয়েছে)। অষ্টাদশ
অধ্যায় কুট্টক ও অন্যান্য প্রণালীর জন্য নিবেদিত যেখানে দ্বি-মাত্রিক অনির্ণীত সমীকরণের (second-degree indeterminate equations) সমাধানও আলোচিত হয়েছে। ব্রহ্মগুপ্ত d x² + a = y² জাতীয় সমীকরণের সমাধান নিয়ে গবেষণা শুরু করেন, যেখানে x, y, a, d পূর্ণসংখ্যা এবং d
পূর্ণবর্গ নয়, যা  বর্তমানে পেল (Pell)-এর সমীকরণ নামে খ্যাত। এই জটিল
প্রশ্নটি, যা সংস্কৃতে ভার্গ প্রকৃতি নামে পরিচিত ছিল, তা বহু শতক ধরে
ভারতীয় গণিতজ্ঞদের অনেক প্রজন্মকে ভাবিয়েছে। অবশেষে জয়দেব একাদশ শতকে এর
সমাধান করেন এবং পরবর্তী কালে দ্বিতীয় ভাস্কর এটির সম্প্রসারণ করেন
‘চক্রবাল’ নামক পদ্ধতির সাহায্যে। ব্রহ্মগুপ্ত নিজে কিছু ক্ষেত্রে এর
সমাধান করেছিলেন এবং দেখিয়েছিলেন যদি এই সমীকরণের একটি সমাধান নির্ণয় করা
সম্ভব হয় তাহলে তার
অসীম সংখ্যক সমাধান নির্ণয় করা সম্ভব হবে। এই সমাধানের পিছনে একটি
অভিন্নতা (identity) ব্যবহার করেছিলেন তিনি, যা বর্তমান গণিতেও ব্যবহৃত হয়
‘ব্রক্ষ্মগুপ্ত অভিন্নতা’ হিসাবে। এগুলি ছাড়াও একবিংশ অধ্যায়ের স্তবকে
ত্রিকোণমিতির আলোচনা আছে। ‘ব্রহ্মস্ফুট সিদ্ধান্ত’ আরব দুনিয়াকে এবং তাদের
মাধ্যমে পরবর্তীকালে ইউরোপের গণিত চর্চাকে যঠেষ্ট প্রভাবিত করেছিল।

দ্বিতীয়
ভাস্কর ছিলেন ‘লীলাবতী’ ও ‘বীজগণিত’ নামের বিখ্যাত গাণিতিক বই
দু’টির লেখক। একজন প্রসিদ্ধ গণিতজ্ঞ ছাড়াও তিনি ছিলেন মহান শিক্ষক এবং
গণিতের প্রচারক। ‘লীলাবতী’-র আক্ষরিক মানে হল হাসিঠাট্টাময় (playful), এবং
এই বইতে কৌতুকের ছলে অঙ্ককে পরিবেশনা করা হয়েছে। এর অনেকগুলো চরণ সরাসরি
এক কম বয়সী সুন্দরী মেয়েকে সম্বোধন করে লেখা, এবং উদাহরণগুলি বিভিন্ন
প্রাণী, গাছপালা ও অলঙ্কারের (ornament) মাধ্যমে বোঝানো হয়েছে। (প্রচলিত
আছে যে লেখক এই বইটির নামকরণ করেছিলেন নিজের মেয়ের নামে, যখন একটি জলঘড়ির
ভুলের কারণে তার বিয়ে ভেঙ্গে যায়। যদিও এর কোন ঐতিহাসিক প্রমাণ
নেই।) গ্রন্থটিতে প্রাথমিক পাটিগণিত, ত্রিভুজ ও চতুর্ভুজের
জ্যামিতি, পীথাগোরাসের সূত্রের প্রয়োগের উদাহরণ, ত্রৈরাশিক, কুট্টক
পদ্ধতি, বিন্যাস ও সমবায়ের সমস্যার উপরে আলোচনা
আছে। ‘বীজগণিত’বইটিতে বীজগণিতের উচ্চ স্তরের আলোচনা রয়েছে, যা ভারতীয়
ঐতিহ্যে এই ধরণের প্রথম মৌলিক প্রচেষ্টা। অজ্ঞাত রাশির সাথে অপারেশন
(operation), কুট্টক ও চক্রবাল পদ্ধতির দ্বারা অজানা সমীকরণের সমাধান এই
রকম আরো কিছু বিষয় উদাহরণ সহকারে আলোচনা করা হয়েছে। ভাস্করের
জ্যোতির্বিদ্যার ওপর লেখা ‘সিদ্ধান্তশিরোমণি’ ও‘করণকুতূহলের’ মধ্যে
ত্রিকোণমিতির অনেক গুরুত্বপূর্ণ ফলাফল এবং ক্যালকুলাসের (কলনবিদ্যা) মত
কিছু ধারণা পাওয়া যায়।

‘সিদ্ধান্ত’ পরম্পরার
অনেক গবেষণাই পরবর্তীকালে সম্পাদিত ও প্রকাশিত হয়েছে এবং অনেকেই এর ওপর
টীকা-টিপ্পনী করেছেন। এদের মধ্যে গত শতাব্দীর অনেকে কাজ আছে, সেই সাথে
কোলব্রুকের (Colebrook) মত ইউরোপীয় লেখকদের কাজ এবং সুধাকর দ্বিবেদী,
কুপ্পান্না শাস্ত্রী ও কে ভি শর্মার মত আরো অনেক ভারতীয়দের কাজও উল্লেখ্য।
 দত্ত ও সিং–এর লেখা দুই খন্ডের বই এবং সরস্বতী আম্মার লেখা বই এই ধরণের
বহু ফলাফলের জন্য সুবিধাজনক রেফারেন্স। কিম প্লোফকারের নতুন বইতেও নানা
বিষয়ে গভীর বিশ্লেষণ সহ পুঙ্খানুপুঙ্খ আলোচনা করা হয়েছে।

প্রাচীন
ভারতীয় গণিতের ইতিহাস অধ্যয়নে ৭০টি ভূর্জপত্র (বার্চ গাছের ছাল) সম্বলিত
বক্ষালী পাণ্ডুলিপি গুরুত্বপূর্ণ অবদান রাখে, যদিও এ নিয়ে অনেক
বিতর্ক আছে। ১৮৮১ সালে পেশোয়ারের কাছে একটি জমিতে খনন কালে এক চাষি এই
পাণ্ডুলিপি উদ্ধার করেন। ভারততত্ত্ববিদ এ এফ আর হর্নলি (A. F. R. Hoernle)
বইটি জোগাড় করে পড়েন এবং এটির বিষয়ে একটি ছোট প্রবন্ধ লেখেন। পরে
পাণ্ডুলিপিটি অক্সফোর্ডের বডলিয়ান গ্রন্থাগারে (Bodleian Library) দান
করেন এবং তখন থেকে সেটি ওখানেই আছে। ১৯২৭ সালে কেয় (Kaye) ভূর্জপত্রগুলির
অনুলিপি (fascimile copies) করেন। অনুলিপিগুলি এই বিষয়ে গবেষণার মূল উৎস
হয়ে ওঠে। প্রথম থেকেই গ্রন্থটির রচনা কাল নিয়ে বিতর্ক আছে, আনুমানিক
সময়কাল খ্রিস্টাব্দ প্রথম শতাব্দী থেকে দ্বাদশ শতাব্দী অবধি হতে পারে।
তাকাও হায়াশির (Takao Hayashi) মতামত এ ব্যাপারে সবচেয়ে নির্ভরযোগ্য, ইনি
এটির রচনাকাল অষ্টম থেকে দ্বাদশ শতাব্দীর মাঝামাঝি বলে চিহ্নিত করেন,
কিন্তু এর গাণিতিক বিষয় খুব সম্ভবত সপ্তম শতাব্দীর। যদিও তেজস্ক্রিয়
কার্বন দিনাঙ্ক (radio carbon dating) দ্বারা এর মীমাংসা সম্ভব কিন্তু এখনো
তা করা হয়ে ওঠেনি।

পাণ্ডুলিপিতে
থাকা বর্গ নয় এমন সংখ্যার বর্গমূল নির্ণয়ের একটি সূত্র প্রভূত দৃষ্টি
আকর্ষণ করেছে। বক্ষালী পাণ্ডুলিপির আর একটি আকর্ষণীয় বৈশিষ্ট এখানে
গণনাগুলিতে বড় বড় সংখ্যার ব্যবহার (দশমিক উপস্থাপনায়)।

অবশেষে
আমরা আলোচনা করব কেরালা ঘরানার কথা। ১৮৩০ সালে চার্লস হুইশ নামে মাদ্রাজের
ইস্ট ইন্ডিয়া কোম্পানির এক ইংরেজ সিভিল সার্ভেন্ট মধ্য কেরালার
(বর্তমানের কোজিকোড়ে থেকে কোচি) প্রাচীন গণিত ঘরানা থেকে এক পাণ্ডুলিপি
সংকলন সবার গোচরে আনেন। দীর্ঘ শিক্ষক-ছাত্র পরম্পরার এই গণিতচর্চার ঘরানাটি
চতুর্দশ শতাব্দীর শেষ থেকে ষোড়শ শতাব্দী পর্যন্ত প্রায় দু’শ বছরের বেশী
স্থায়ী ছিল। মাধবের সময় থেকে এর শুরু বলে মনে করা হয় এবং পরবর্তী
লেখকরাও তাঁকেই বহু গবেষণার কৃতিত্ব দিয়ে গেছেন। মাধব ছাড়াও নীলকণ্ঠ
সোময়াজি হলেন এই ঘরানার আরও একজন বিশিষ্ট ব্যক্তিত্ব। বর্তমানে মাধবের
গণিত সংক্রান্ত অবদানের মূল উৎসগুলি আর কিছু অবশিষ্ট নেই (যদিও কিছু
জ্যোর্তিবিদ্যার কাজ এখনো আছে)। নীলকণ্ঠ ১৫০০ সালে ‘তন্ত্রসংগ্রহ’
(সংস্কৃতে) নামে একটি বই লেখেন। এই ঘরানা থেকে বহু ভাষ্য প্রকাশিত হয়েছে
যার মধ্যে শঙ্করের লেখা ‘যুক্তিদীপিকা’ ও ‘ক্রিয়াক্রমকারী’ এবং মালয়ালম
ভাষায় জ্যেষ্ঠদেবের লেখা ‘যুক্তিভাষা’ উল্লেখযোগ্য। বিংশ শতাব্দীর মধ্যভাগ
থেকে বহু ভারতীয় গবেষক এই সমস্ত পাণ্ডুলিপি নিয়ে গবেষণা করেছেন এবং
প্রায় সমস্ত পাণ্ডুলিপি পরীক্ষণ করেছেন। কে ভি শর্মা একটি সম্পাদিত অনুবাদ
প্রকাশ করেন যেটি বর্তমানকালে ব্যাখ্যামূলক মন্তব্য সহকারে কে
রামসুব্রহ্মণ্যম, এম ডি শ্রীনিবাস এবং এম এস শ্রীরাম প্রকাশ করেন। সম্প্রতি
কে রামসুব্রহ্মণ্যম ও এম এস শ্রীরাম ‘তন্ত্রসংগ্রহ’র একটি অনুবাদ সম্পাদনা
করেন।

কেরালার
গণিত চর্চা অতীত বিশ্বের যেকোন স্থানের তুলনায় একটি উচ্চ পর্যায়ে উন্নিত
হয়েছিল। যদিও এখানে উল্লেখ্য যে চৈনিক গবেষণাও কিছু কৃতিত্বের দাবিদার,
যা অবশ্যই বিশ্লেষণ করার প্রয়োজন আছে। কেরালার অবদান π-এর ক্রম সম্প্রসারণ
ও চাপ-স্পর্শক ক্রম এবং সাইন ও কোসাইন (sine and cosine) অপেক্ষকের ক্রম
নির্ণয় যা প্রায় দুই শতাব্দী পরে ক্রমানুসারে জর্জ, লিবনিজ ও নিউটনের হাত
ধরে ইউরোপে প্রকাশিত হয়। π-এর একাদশ দশমাংশ পর্যন্ত সঠিক সংখ্যাগত মান এই
কাজ গুলির অন্যতম অবদান। অনেক ভাবেই কেরালার গণিতজ্ঞরা কলনবিদ্যা বা
ক্যালকুলাস পূর্বানুমান করতে পেরেছিলেন পরে যা ইউরোপে বিকাশ লাভ করে,
বিশেষত বৃত্তের পরিধি নির্ণয়ে অপরিমেয় ক্ষুদ্রর বিবেচনা কলনবিদ্যার
ক্ষুদ্রাতিক্ষুদ্র ধারণার সমতুল্য। কিছু লেখক মনে করেন এটি ততদিনে
কলনবিদ্যারই রূপ পেয়েছে।  

এই
সমৃদ্ধ গণিত ঐতিহ্যের যথাযত মান্যতার জন্য এখনও অনেক কিছু করার আছে।
অদ্যপি বর্তমান পাণ্ডুলিপিগুলির ক্ষয় থেকে রক্ষার জন্য সঠিক যত্ন,
রক্ষণাবেক্ষণ ও সমস্ত সাম্প্রতিকতম তথ্য সংযোজন করা এবং সর্বোপরি
নৈর্ব্যক্তিক দৃষ্টিকোণ থেকে যথাযত চর্চার দ্বারা গাণিতিক উপলব্ধিগুলি
বিশ্ব গণিত মানচিত্রে উপযুক্ত স্থান দেওয়া প্রয়োজন। আশা করা যায় এই
প্রচেষ্টা আমাদের মধ্যে সঞ্চারিত হয়ে এই মহান কাজে ব্রতী করে তুলবে।
অন্যথায় মিথ্যা অপপ্রচারে এসব কিছু বিনষ্ট হবে।

• ডাঃ কালী প্রদীপ চৌধুরীর না জানা ইতিহাস, বর্তমানে স…
• পৃথিবীর সর্বশ্রেষ্ঠ বেদবিদ ,ধর্মজ্ঞ ,মহাত্মা , জ্য…
• ইতিহাসের এক ভষ্কর অধ্যায় তৈমুর লং……………….
• বিজ্ঞানী নিউটনের পূর্বে বিজ্ঞানী ভাস্করাচার্য কি…
• আমাদের গণিত, গণিতের আমরা: মজার গণিতের সন্ধানে। লেখ…
• ক্যালকুলেটর ছাড়াই বড় বড় গণিত সমাধান করা সম্ভব ?? দ…
• কৃত্রিম কিডনি বানিয়ে চমক বাঙালি, বাজারে আসতে চলেছে…
• বেতার-বার্তায় বিপ্লব: বাঙালির বিজ্ঞানী কৌশিক ……..
• মহাকাশে এ বার ‘রূপকথা’ লিখবেন এই বঙ্গনারী! ……….
• নিজেই চলবে বাইক ! এ সাফল্য বাঙ্গালী হাত ধরেই………
• ইতিহাসে ভারতীয় উপমহাদেশে……………………….
• উপমহাদেশের বিজ্ঞানী আনন্দ কান্নন, সদ্যোজাতদের জন্ড…
• নয়া আদিপুরুষের খোঁজ দিলেন বাঙালি
• সিন্ধু সভ্যতার বয়স ৫৫০০ নয়, ৮০০০ বছর! বলছে নতুন গব…
• বাঙালি হাত ধরেই মহাকর্ষীয় তরঙ্গের আবিষ্কার………..
• মানুষ তো বিভিন্ন দেশে যায় কিন্তু এদেশে কাওকে যেতে …
• বর্তমান সময়ের বিশ্বের বিজ্ঞানী সমাজের পথপ্রদর্শক,ব

অতিরিক্তঃ 

১।
অনুবাদকের সংযোজন – ‘বৃত্তীয় চতুর্ভুজ’ (cyclic quadrilateral) হল এমন
একটি চতর্ভুজ যার চারটি শীর্ষবিন্দু একটি বৃত্তের পরিধির উপর অবস্থিত।

লেখক পরিচিতি: ডঃ
এস জি দানি বর্তমানে ‘স্কুল অফ মাথেমেটিক্স’, টিআইএফআর, মুম্বই-এর প্রফেসর
এবং আইআইটি, বম্বে-র গণিত বিভাগের ভিজিটিং প্রফেসর পদে গবেষণারত। মুম্বই
ইউনিভার্সিটি থেকে ১৯৬৯ সালে এমএসসি করে উনি টিআইএফআর, মুম্বাই থেকে ১৯৭৫
সালে পিএইচডি করেন। তাঁর গবেষণার স্বীকৃতি স্বরূপ ১৯৯০ সালে তাঁকে ‘ভাটনগর’
পুরস্কারে সন্মানিত করা হয়। ২০০৭ সালে তিনি ‘ওয়ার্ল্ড অ্যাকাডেমি অফ
সায়েন্স’ পুরস্কারও লাভ করেন।