 সভ্যতার উৎসভূমি আমাদের এই এশিয়া। ধর্ম দর্শন বিজ্ঞান প্রযুক্তি- সবকিছুরই
সভ্যতার উৎসভূমি আমাদের এই এশিয়া। ধর্ম দর্শন বিজ্ঞান প্রযুক্তি- সবকিছুরইশেকড় এশিয়ার
মাটিতে গভীরভাবে প্রোথিত। আমরা জানি সকল বিজ্ঞানের ভিত্তি
অঙ্ক। আর অঙ্কের ভিত্তি হচ্ছে শূন্য। বর্তমান বিজ্ঞানের জননী ‘শূন্য’
আবিষ্কার করেন ব্রহ্মগুপ্ত (598–668 AD)। বর্তমান ডিজিটাল যুগ পুরোপুরিই
নির্ভর করছে ব্রহ্মগুপ্তের শূন্য-এর উপর। ব্রহ্মগুপ্ত একটি সুবিখ্যাত বই
রচনা করেন, পরবর্তীতে এই বইয়ের নাম দেন ‘ব্রহ্মস্ফুট সিদ্ধান্ত’
(Correctly Established Doctrine of Brahma)। রচনাকাল আনুমানিক
৬২৮
খ্রিষ্টাব্দ। এই উপমহাদেশের গণিত ও জ্যোতির্বিজ্ঞানের সঙ্গে আরব দুনিয়ার
সর্বপ্রথম পরিচিতি হয় এই ‘ব্রহ্মস্ফুট সিদ্ধান্ত’-এর মাধ্যমে।
কঙ্ক
নামে উজ্জ্বয়িনীর এক পণ্ডিত আনুমানিক ৭৭২ খ্রিস্টাব্দে বাগদাদে খলিফা আল
মনসুরের দরবারে একটি ‘ব্রহ্মস্ফুট সিদ্ধান্ত’ নিয়ে যান। আল ফাজারি খলিফার
অনুরোধে কঙ্কের সাহায্যে তর্জমা করে আরবি ভাষায় অনুবাদ করে ও বইটিকে নাম
দেন ‘জিজ-আল সিন্ধিন্দ’ (সিন্ধিন্দ= সিদ্ধান্ত)। পরে আল খোয়ারিজমি
‘আল-কিতাব আল-মুখতাসার ফি হিসাব আল-জাবর ওয়া আল-মুকাবালা’ (الكتاب المختصر
في حساب الجبر والمقابلة ) লেখবার সময় এই বইটি (জিজ আল সিন্ধিন্দ)
ব্যবহার করেন। শূন্য প্রসঙ্গে বাংলার দার্শনিক বা গাণিতিক ব্যাখ্যা প্রথমে
বুঝতেই পারেন নি জন ওয়ালিস বা বিশপ বার্কলের মতো ইউরোপিয়ান গণিতজ্ঞরা।
শূন্যকে তারা ব্যাখ্যা করেছিলেন non–number হিসেবে।
অথচ আমাদের
বাংলায় শূন্যকে উপলব্ধি করেছে হাজার বছর আগে। শূন্যের পাটিগণিত, the
arithmetic of zero, গাণিতিক বিজ্ঞানে সম্পূর্ণই আমাদের অবদান। মিসর নয়,
গ্রিস নয়, শুধুই বাংলাই শূন্যকে নিয়ে এইভাবে ভাবতে পেরেছিলো। প্রাচীন
মুনি কণাদ এই শূন্যকে নিয়ে অনেক কথা লিখেছেন। শূন্যকে তিনি ব্যাখ্যা
করেছেন তার নিজস্ব উপলব্ধির আলোয়। ব্রহ্মগুপ্তই প্রথম গণিতশাস্ত্রে
পাটিগণিত এবং বীজগণিতের প্রচলন করেন। এছাড়াও তিনি ব্রহ্মস্ফুট সিদ্ধান্তে
লিনিয়ার ইকুয়েশান (Liner equation) কোয়াড্রেটিক (Quadratic equation)
এবং Indeterminate equation, interpolation formula ও বিশেষ ধরনের
ডায়োফ্যান্টাইন সমীকরণের (Diophantine equation) সমাধান নিয়ে নতুন
পদ্ধতিতে আলোচনা করেন। বলতে পারেন আধুনিক বিজ্ঞান পুরোপুরি বাংলার সংখ্যা
পদ্ধতির ওপর দাঁড়িয়ে আছে।


 শিল্পীর চোখে ব্রহ্মগুপ্ত
শিল্পীর চোখে ব্রহ্মগুপ্ত



ব্রহ্মগুপ্ত


ব্রহ্মগুপ্ত
কণাদ
(600 BCE) সর্বপ্রথম পরমাণু সম্পর্কে বক্তব্য প্রদান করেছিলেন। তিনি তার
বৈশেষিক সূত্র বইটিতে পরমাণু চিন্তার প্রকাশ করেছিলেন এবং এই সম্বন্ধে বিশদ
আলোচনা করেছেন। তিনি বস্তুর অভ্যন্তরীণ গঠন নিয়ে চিন্তা ভাবনা করে বলেন
প্রতিটি বস্তুই পরমাণু দ্বারা সৃষ্টি হয়েছে। তিনি বলেন, Every object of
creation is made of atoms which combine to form molecules. তার এই পরমাণু
তত্ত্ব তিনি দিয়েছিলেন বিজ্ঞানী জন ডাল্টন এরও আড়াই হাজার বছর আগে। কণাদ
কার্যকারণ তত্ত্ব (law of causation) ব্যাখ্যা করে বলেছেন, Every effect
is a fresh creation or a new beginning. বিখ্যাত ঐতিহাসিক T.N. Colebrook
বলেন, ‘Compared to the scientists of Europe, Kanad and other Indian
scientists were the global masters of this field.’



কণাদ (600 BCE) সর্বপ্রথম পরমাণু সম্পর্কে বক্তব্য প্রদান করেছিলেন।
প্রাচীনকালে আমাদের এই উপমহাদেশে জ্যামিতি, গণিত, আধ্যাত্মিকতা ও ধর্মের
বিভিন্ন রীতির এক অদ্ভুত সংমিশ্রণ ঘটেছিলো। বলা যেতে পারে গণিত এবং
বিজ্ঞানের ইতিহাসে সারা পৃথিবীতে আমাদের প্রাচীন পণ্ডিতরাই ছিলেন মূলত
অগ্রপথিক।
পিথাগোরাসের উপপাদ্য আবিষ্কারের অনেক আগেই প্রাচীন ভারতে
এ উপপাদ্য অপাস্তমব্য উপপাদ্য নামে পরিচিত ছিলো। এই সুতিকাগারেই আবিষ্কৃত
হয় ডেসিমাল নাম্বার সিস্টেম। দশমিক পদ্ধতি ব্যবহার সর্বপ্রথম আর্যভট্ট
(476–550 CE) করেন। তিনি বলেন দশমিক পদ্ধতিতে শূন্যর মান নিয়েই অন্যান্য
অঙ্কের স্থানীয় মান নির্ধারিত হয়। যেখানে ৪৯৮ সালে তিনি বলেন স্থানম
স্থানম দশ গুণম অর্থাৎ স্থান বদলালে মান বারে দশ গুণ।
আর্যভট্ট
(476–550 CE) ছিলেন প্রাচীন ভারতের একজন সর্বশ্রেষ্ঠ জ্যোতিবিজ্ঞানী।
কোপারনিকাস এবং ব্রুনোর হাজার বছর আগে প্রাচীন আর্যভট্টের কাজের পদ্ধতি
ছিলো সূর্যকেন্দ্রিক। হিন্দু পৌরাণিক ধারণার পরিবর্তে সূর্যগ্রহণ এবং
চন্দ্রগ্রহণের প্রকৃত কারণগুলো তিনি ব্যাখ্যা করে গেছেন। সেই সাথে সূর্য
গ্রহণ এবং চন্দ্রগ্রহণের সময়কাল নির্ণয়ের পদ্ধতিও বের করেছিলেন। আর্যভট্ট
বলেছিলেন যে, চাঁদের আলো আসলে সূর্যের আলোর প্রতিফলনেরই ফলাফল। তিনি তার
আর্যভট্টীয় গ্রন্থে ভূ-ভ্রমণবাদের কথা বলেছেন। তিনি বলেন, ‘স্রোতের অনুকূল
গতিবিশিষ্ট নৌকা রুঢ় ব্যক্তি যেমন তীরস্থ অচল বস্তুসমূহকে প্রতিকূলগামী
দেখেন তেমনি নিরক্ষ অঞ্চলে অচল নক্ষত্রসমূহকে সমবেগে পশ্চিমগামী দেখা
যায়’।
গতির কারণ যে এক প্রকার আকর্ষণী বল সে সময় তিনি তা উপলব্ধি
করতে পেরেছিলেন। গ্রহদের গতি ব্যাখ্যা করার জন্যে তিনি টলেমীর পরিবৃত্ত
এবং উৎকেন্দ্রিক ধারনা গ্রহণ করে ছিলেন। তিনি উদাহরণের মাধ্যমে আর্যভট্টীয়
বইটির গোলপাদ অংশে বলেছেন যে পৃথিবী নিজ অক্ষের সাপেক্ষে ঘোরে। পৃথিবীর
আক্ষিক গতির হিসেবও আর্যভট্ট বের করে করেছিলেন। তার হিসেব মতে পৃথিবীর
পরিধি ছিলো ৩৯,৯৬৮ কিলোমিটার। এই হিসেব সে সময় পর্যন্ত বের করা যেকোনো
পরিমাপের চেয়ে শুদ্ধতর (ভুল মাত্র ০.২%)। তিনি আর্যভটীয় নামক গ্রন্থে
দ্বিঘাত প্রথম মাত্রার অনির্ণেয় সমীকরণের সমাধান ও π এর মান এর উল্লেখ
করেন। তিনি পাইয়ের মান বের করতে গিয়ে লিখেছেন ‘চার এর সাথে একশ যোগ করে
তাকে আট দিয়ে গুণ করে তার সাথে বাষট্টি হাজার যোগ করা হলে বিশ হাজার একক
ব্যাসের বৃত্তের পরিধি পাওয়া যায়’। এই হিসেবে আমরা পাই
(4+100)×8+62000)/20000 = 62832/20000 = 3.1416, এই হিসেব তার সময় পর্যন্ত
যেকোনো গণিতবিদের বের করা মানগুলোর মাঝে সবচেয়ে সঠিক।






শিল্পীর চোখে আর্যভট্ট


পুনে অবস্থিত Inter-University Centre for Astronomy and Astrophysics (IUCAA)-এ আর্যভট্টের ভাস্কর্য
প্রাচীন
ভারতের আর একজন বিজ্ঞানী গণিতবেত্তা ছিলেন ভাস্করাচার্য (1114–1185)।
তিনিই সর্বপ্রথম গণিতশাস্ত্র অসীম (Infinity) কথাটি প্রবর্তন করেন। তিনি
সর্বপ্রথম বলেন, কোনো সংখ্যাকে শূন্য দ্বারা ভাগ করলে এই অসীম পাওয়া যায়।
বিজ্ঞানী ভাস্করাচার্য অন্তরকলন গননা (Differential calculus) প্রক্রিয়ার
প্রাথমিক ধারণা দেন এবং এর পরবর্তীতে নিউটন এবং লাইবনিজ অন্তরকলন আবিষ্কার
করে গণিতে নব যুগের সূচনা করেন। বিজ্ঞানের রাজ্যে ঘটে বিপ্লব। এছাড়াও
ভারতীয় গণিতবিদ গোবিন্দ স্বামী ‘ইন্টারপোলেশন ফর্মূলা’ (Interpolation
formula) ও ভটৈশ্বরাচার্য ব্যাকওয়ার্ড ইন্টারপোলেশন ফর্মূলা’ (Backward
Interpolation formula) ও নীলকান্ত মুণি ‘সমধর্মী ক্রম’ (Infinite
Geometric Progression convergent series) নিউটনের বহু আগেই ব্যবহার করেন।
পঞ্চম
শতাব্দীর শেষে রাজা বিক্রমাদিত্যর নবরত্ন সভার অন্যতম রত্ন বরাহমিহির
(505–587 CE), তিনি তার বৃহৎসংহিতা বইয়ে আধুনিককালের সিমেন্টের মত ব্রজলেপ
নামে একটি বস্তুর প্রস্তুতপ্রণালী ব্যাখ্যা করেছেন। ভারতে সে সময়
বরাহমিহির উদ্ভাবিত এই ব্রজলেপ দিয়েই বড় বড় দালান কোঠার ইটের গাঁথুনি
তৈরীতে ব্যবহৃত হতো। ‘পঞ্চসিদ্ধান্তিকা’ গ্রন্থে sin30 ও sin 60 এর মান
নির্ণয় করে দেখিয়েছেন। বরাহমিহির n সংখ্যক বস্তু থেকে r সংখ্যক বস্তু
পছন্দ করার সমস্যা তথা “সমাবেশ”-এর (Combination) সমস্যাটিকে নতুন একধরনের
সারণীর মাধ্যমে করেন। পরবর্তীতে তার এই সারণীটিই পাস্কালের ত্রিভুজ”
(Pascal’s triangle) নাম নিয়ে অনেক শতাব্দী পরে ইউরোপে পুনরাবিষ্কৃত হয়।
বর্তমান ত্রিকোণমিতিতে ব্যবহৃত মূল সূত্রগুলিও বরাহমিহির এর আবিষ্কার।
আমরা বলতে পারি পাশ্চাত্যের সকল জ্ঞান ও প্রযুক্তির উৎসভূমি এশিয়া। এর রয়েছে এক গৌরবোজ্জ্বল সোনালি ইতিহাস।










নতুন গণিত !!!
প্রাচীন
ভারতে এক ধরনের গণিতের প্রচলন ছিলো যা কালের আবর্তে হারিয়ে গিয়েছিলো। গত
বিংশ শতাব্দীর প্রথম দিকে এই গণিতের নতুন করে অর্থ উদ্ধার করা হয়। শ্রী
ভারতী কৃষ্ণ তীর্থজি নামে ভারতের পুরীর (Puri) একজন ধর্মীয়গুরু যিনি গণিত,
ইতিহাস, দর্শন এবং সংস্কৃত এর পণ্ডিত ছিলেন, তিনি ১৯১১ থেকে ১৯১৮ সাল
পর্যন্ত নানা গবেষণা করেন এবং গভীর ধ্যানে নিমগ্ন হয়ে বেদ থেকে ১৬টি
গণিতের সূত্র লিপিবদ্ধ করেন। পরবর্তীতে এর নাম দেন সূত্রাবলি। ১৯৬৫ সালে
সুত্রাবলি নিয়ে “বৈদিক গণিত” নামে একটি বই প্রকাশ করেন। অবশ্য তিনি বলেন
যে বর্তমান বেদের মধ্যে এই সুত্রগুলো খুঁজে পাওয়া যাবে না। তিনি তাঁর
সজ্ঞা দ্বারা বেদের বিভিন্ন জায়গায় ছড়ানো ছিটানো রূপক গোপন সংকেত একত্র
করে সূত্রকারে গ্রন্থিত করেন। বলা হয়ে থাকে ভারতী কৃষ্ণ লেখা ১৬ খণ্ডে এই
বইয়ের মাধ্যমে বৈদিক যুগের হারানো গণিতের সন্ধান পাওয়া গেছে। এক খণ্ডে এই
চমৎকার বইটি প্রকাশিত হয় তার মৃত্যুর পাঁচ বছর পর।


সাধনারত অবস্থায় তীর্থজি



তার
গবেষণা মতে, গণিত ১৬টি সূত্রের উপর প্রতিষ্ঠিত। এই ফর্মুলাগুলো আমাদের
মনের স্বাভাবিক প্রকৃতির সাথে জড়িত থাকে ফলে খুব দ্রুত হিসেব করে সমাধানের
পথে এগিয়ে যাওয়া যায়। এই গণিতের সব চেয়ে গুরুত্বপূর্ণ বৈশিষ্ট্য হচ্ছে
এটির প্রাঞ্জলতা এবং গতিময়তা। বিভিন্ন প্রকারের সূত্রের মারপ্যাঁচের
চেয়ে এই গণিত একে অপরের সাথে সঙ্গতিপূর্ণ এবং ঐক্যবদ্ধ। সাধারণ যোগ বিয়োগ
গুণ ভাগ, স্কোয়ার রুট সাধারণত এক লাইনের মধ্যেই সহজে করা যায়। এটির ফলে
শিক্ষার্থীর মনের উপর কোনো চাপ পড়ে না এবং তাই তারা নতুন নতুন চিন্তা
ভাবনার প্রসার ঘটাতে পারে। এই গণিত ব্যবহারের ফলে অনেক কঠিন এবং জটিল
সমস্যাকে তাৎক্ষণিকভাবে সমাধান করা যায়। এই আকর্ষণীয় এবং চমৎকার
পদ্ধতিগুলো আধুনিক গণিতের চাইতে অনেক বেশি সুশৃঙ্খল।
ষাট এর দশকের
শেষের দিকে যখন এই বৈদিক গণিত ব্রিটেনে যায় তখন বিকল্প গণিত হিসেবে এটি
দ্রুত স্থান করে নেয়। বিখ্যাত ব্রিটিশ গণিতবিদদের মধ্যে অনেকেই এই গণিতের
ব্যাপারে আগ্রহ প্রকাশ করেন। এর মধ্যে রয়েছেন কেনেথ উইলিয়ামস, এন্দ্রু
নিকোলাস এবং জেরেমি পিকেলস। এই গণিতবিদরা ভারতী কৃষ্ণের বইটিকে পরিবর্তন ও
পরিমার্জন করে ১৯৮১ সালে লন্ডনে সিরিজ লেকচার প্রদান করেন এবং পরবর্তীতে
সিরিজ লেকচার সঙ্কলিত করে প্রকাশিত হয় Introductory Lectures on Vedic
Mathematics। এন্দ্রু নিকোলাস এই গণিতের উপর গবেষণা করতে ভারতে ১৯৮১-১৯৮৭
সাল পর্যন্ত বেশ কয়েকবার যাতায়াত করেন। পরবর্তীতে তার আগ্রহে এই পদ্ধতিটি
ভারতের বোদ্ধা এবং শিক্ষিত সমাজের নজর কাড়তে সক্ষম হয়।
এই
গণিতের সরলতা হচ্ছে এটিকে আপনি মনে মনে করে ফেলতে পারবেন। অবশ্য আপনি লিখেও
ফেলতে পারবেন। এই মানসিক কোমল এবং নমনীয় পদ্ধতি ব্যাবহারের ফলে যে কেউ
গণিতে নিজস্ব পদ্ধতি আবিষ্কার করতে পারবে, তারা কেউ কোনো নির্দিষ্ট পদ্ধতির
বন্ধনে আবদ্ধ থাকবে না। ফলে ব্যক্তি এগিয়ে যাবে সৃজনশীলতার এক আকর্ষণীয়
পথে। এই সূত্রগুলো গণিতের প্রতিটি ক্ষেত্রে যেমন আলজেব্রা, জ্যামিতি (plane
and solid), ত্রিকোণমিতি (plane and spherical) conics – geometrical and
analytical, জ্যোতির্বিজ্ঞান, ক্যালকুলাস (differential and integral) খুব
দ্রুত ও সংক্ষিপ্ত পদ্ধতিতে সমাধান করতে পারে। বলতে পারি সর্ব প্রকার
গণিতের জন্যে এই পদ্ধতিটি কার্যকর।
ক্রমবর্ধমান জনপ্রিয়তা
শ্রেণীকক্ষে
গণিতের শিক্ষক সহজ এবং বিকল্প পদ্ধতির কথা দীর্ঘ দিন ধরে ভাবছিলেন। শিক্ষা
ক্ষেত্রে বৈদিক গণিত খুব দ্রুত স্থান দখল করতে সক্ষম হয়। বর্তমান ভারত সহ
পৃথিবীর বিভিন্ন দেশে শিক্ষাঙ্গনে এই গণিতের ব্যাপক চর্চা চলেছে।
ইংল্যান্ডের সেইন্ট জেমস ইন্ডিপেনডেন্ট জুনিয়র স্কুল, সেইন্ট জেমস
ইন্ডিপেনডেন্ট স্কুল ফর বয়েজ, সেইন্ট জেমস ইন্ডিপেনডেন্ট স্কুল ফর গার্লস,
লিডস এ আলকুইন স্কুল, এছাড়া সিডনীর জন কোলেট স্কুল, আমেরিকার দি আব্রাহাম
লিঙ্কন স্কুল, ডাবলিনের জন স্কটাস স্কুল, সাউথ আফ্রিকার সেন্ট জেমস স্কুল,
মেলবোর্নের ইরাসমাস স্কুল, নিউজিল্যান্ডের ফিচিনো স্কুলসহ আর নানা স্কুলে
এই গণিতের উপর পাঠদান চলছে।
বর্তমানে ভারত সরকার এই গণিত প্রসারের
জন্যে ব্যাপক উদ্যোগ গ্রহণ করেছে। IIT Indian Institute of Technology
(IIT) তে এই গণিতের উপর চর্চা চলছে এবং তারা ব্যাপক উপকৃত হচ্ছে। শিশুদের
উপর বিভিন্ন গবেষণায় দেখা গেছে শিশুদের অঙ্ক ভীতি দুর হয়ে গেছে। এই
গণিতের চর্চা করে জ্যামিতি, ক্যালকুলাস গণিতের উচ্চতরক্ষেত্রে চিন্তার
সরলতা এবং মেধার বিকাশ ঘটাতে পারছে। অবশ্য এই গণিতের সৌন্দর্য এবং
কার্যকারিতা নির্ভর করে চর্চার উপর। চর্চা করলে যে কেউ এটি আবিষ্কার করতে
পারে আধুনিক কালের সবচেয়ে সহজ এবং মজার গণিতকে।



Dr cassells এর সাথে মহাঋষি স্কুলের কোমলমতি শিক্ষার্থীরা
পাঠ্যপুস্তকে নতুন গণিত
১৯৮৮
সালে মহাঋষি মহেশযোগী এই গণিতের সৌন্দর্যের কথা বলেন। সারা পৃথিবীর
বিভিন্ন জায়গায় অবস্থিত ১০০টিরও বেশি মহাঋষি স্কুলের সিলেবাসে এই গণিত
অন্তর্ভুক্ত করেন। আমেরিকায় Maharishi University of Management-এ এই এই
গণিত এখন ব্যাপকভাবে অর্থনীতি ও MBA ছাত্রদের শেখানো হচ্ছে। এর ফলে তাদের
গণিতের উপর দখল যাচ্ছে বেড়ে। সারা পৃথিবীতে মহাঋষি স্কুলের ১০০টির উপর
সিলেবাসে অন্তর্ভুক্ত করে। ইংল্যান্ডে লাঙ্কাশাইয়েরে স্কেলমার্সডেল
(Skelmersdale)-এ ১১-১৪ বছরের ছাত্রছাত্রীর জন্যে “কসমিক কম্পিউটার” নামে
পুরো একটি কোর্স চালু করেন। পরবর্তীতে কসমিক ক্যালকুলেটর” নাম দিয়ে ১৯৮৮
সালে এই কোর্সটি বই আকারে প্রকাশিত হয়।
Lancashire-এ মহাঋষি
স্কুলে ৩ স্তরে এই গণিত শিক্ষা দেয়া হয় যা সেই দেশে জাতীয় পাঠ্যক্রমকে
(national curriculum) কভার করে। এটি প্রয়োগ করার ফলে স্কুলের বাচ্চাদের
মনে গভীর দাগ কাটে। গণিত ভীতি কেটে যায় যার ফলে তাদের একাডেমিক
পারফর্মেন্স আগের তুলনায় অনেক বেড়ে বৃদ্ধি পেয়েছে। এই কোর্সের পর তাদের
GCSE পরীক্ষায় সবাই A grade এ পাস করে। কেনেথ উইলিয়ামস GCSE এবং ‘A’
লেভেল পরীক্ষায় কীভাবে এই গণিত প্রয়োগ করে সমাধান করা যায় তা নিয়ে
অনেকগুলো বই প্রকাশ করেছেন। এছাড়া ত্রিকোণমিতি, non-linear partial
differential equations, simultaneous equations সিরিজ, Quadratic
Equations নিয়েও আলাদা আলাদা প্রকাশনা রয়েছে।
[






সিডনীর জন কোলেট স্কুলের ক্ষুদে শিক্ষার্থীরা






(Skelmersdale)এ “কসমিক কম্পিউটার” পাঠদানকালে আনন্দরত শিক্ষার্থীরা



মহাঋষি স্কুলে গণিতের সাথে ধ্যানরত অবস্থায়


মহাঋষি স্কুলের লোগো
এই গণিত একাধারে কোমল এবং নমনীয়। মানস চক্ষে দেখা যায় পরিষ্কার।
creativity খুব দ্রুত বাড়ানো যায় এই পদ্ধতির সাহায্যে। শিশুদের যাদের
অঙ্কভীতি রয়েছে তাদের কাছে এই পদ্ধতিটি অত্যন্ত উপাদেয় মনে হবে। ফলে
স্কুলে এবং অন্যান্য ক্ষেত্রে একাডেমিক পারফর্মেন্স বৃদ্ধি করা সম্ভব হয়।
এই গণিত আমাদের বুদ্ধিবৃত্তিক মনন এবং মনোযোগ বৃদ্ধিতে সহায়তা করে। বলা
হয় সাধারণ গণিতের চাইতে এটি ১৫০০% দ্রুত সম্পন্ন করা যায়। বিভিন্ন
প্রতিযোগিতামূলক পরীক্ষায় সময় বাচায় এবং ফলাফল সম্বন্ধে নিশ্চিত হওয়া
যায়। অভিজ্ঞতায় দেখা গেছে এই গণিত ৮ থেকে ১২ মাস নিয়মিত চর্চা করলে
বর্তমান দেশী এবং বিদেশী ইউনিভার্সিটির ১৫-২০ বছরের গণিতের পুরো কোর্স
সম্পন্ন করা সম্ভব হয়। যেকোনো বয়সের মানুষের জন্যে এই গণিত অত্যন্ত
সুস্বাদু বলে মনে হবে।
আমাদের দেশে অবশ্য এই গণিতের প্রয়োগ দেখা
যায় না। আমরা আশা করছি মহাঋষি স্কুলের মতো আমাদের দেশেও একদিন চর্চা শুরু
হবে এই গণিতের। গণিতভীতি কাটিয়ে আমাদের অনন্যতা ছড়িয়ে যাবে পৃথিবীর
সবদিকে। আমাদের অতীত মহান ছিলো, তাই সব সময় মনে মনে এই অটো সাজেশনটি বলুন,
আমি এক অনন্য মানুষ আমরা এক মহান জাতি।
আসুন দেখে নেই এই গণিতের কিছু অন্তনিহিত সৌন্দর্যকে……
আপনি কি ৩ সেকেন্ডের মধ্যে মনে মনে এই অঙ্কটি করতে পারবেন ?
52 x 11 = ____ ____ ____
এটি অত্যন্ত সহজ। একটু চেষ্টা করে দেখুন। আমরা জানি আপনি পারবেন। সময় শেষ আপনার
উত্তর হচ্ছে: 572
কীভাবে !!
৩
সেকেন্ডে বের করতে না পারলেও চিন্তার কিছু নেই! কারণ এক মিনিট পর থেকেই
আপনি যেকোনো দুই ডিজিটের নাম্বারকে ১১ মনে মনে মুখে মুখেই, চিন্তা ছাড়াই ২
সেকেন্ডের মধ্যে করে ফেলতে পারবেন।
লক্ষ্য করুন,
52 x 11 = ____ ____ ____
প্রথমে
সংখ্যাটি লিখুন এবং মাঝে একটি ফাঁকা জায়গা রাখুন অর্থাৎ 5 ____ 2। এবার
মনে মনে যোগ করে দিন (5+2=7)। এই 7 কে 5 ____ 2 এর মাঝে বসিয়ে দিন।
আপনার কাজ শেষ, তাহলে উত্তর হলো 5 7 2
আবার প্রথম থেকে দেখুন। কত সহজ !! তাই না ![]()
আবার দেখুন,
43 x 11 =473
প্রথম ধাপ,
43 এর মাঝে ফাঁকা জায়গা রাখুন; 4 ____ 3
দ্বিতীয় ধাপ,
এই বার যোগ করুন (4+3=7)
তৃতীয় ধাপ,
4 ____ 3 এর মাঝে 7 বসিয়ে দিন; উত্তর হবে 473 ![]()
আবার প্রথম থেকে দেখুন
এবার মুখে মুখে ২ সেকেন্ডে উত্তর বলুন।
72 x 11=?
27 x 11=?
25 x 11=?
কত সহজ তাই না !!
হুম, বুঝলাম কিন্তু এবার এই অঙ্কটি করুন তো 75 x 11=____ ____ ____
হিসেব মতো এবার হয় (7+5=12)
12কে মাঝে বসিয়ে দিলে হয়,
7 12 5
এটি কি সঠিক উত্তর ? না এটি সঠিক হয় নাই। উত্তর ভুল ![]()
এটি কীভাবে করতে হবে !!
চিন্তার
কিছু নাই। এই সব সময় মনে রাখুন, সভাপতির চেয়ারে এক জনই বসতে পারে (দু জন
বসলে সভার অবস্থা কী হবে তা একবার ভেবে দেখুন), মাঝের ফাঁকা স্থানটিতে
একটি সংখ্যাই বসতে পারে। তাহলে কী হবে?? চিন্তার কিছু নেই, উদোর পিণ্ডি
বুধোর ঘাড়ে দিয়ে দিন। যদিও নিজের দোষ অন্যের ঘাড়ে চাপিয়ে দেয়া বিরাট
অন্যায়। তবে অঙ্কে এটি জায়েজ আছে। (অতি সতর্কতা, এটি কোনো ফতোয়া নয়,
আপনারা কী বলেন?) তবে সবসময় সতর্ক থাকুন, যেন অন্য কেউ তার দোষ আপনার
ঘাড়ে চাপাতে না পারে। এর জন্যেই কৌশল জানা দরকার। অঙ্কে এই চাপিয়ে দেয়ার
কৌশলটি হচ্ছে, যোগফলের প্রথম সংখ্যাটিকে (১২ এর ১ কে) পাশের জনের ঘাড়ে
দিয়ে দিন এবং পরে যোগ করুন।
এবার দেখুন,
75 x 11= ____ ____ ____
প্রথম ধাপ,
75 এর মাঝে একটি ফাঁকা জায়গা রাখুন 7 ____ 5
দ্বিতীয় ধাপ,
এবার সংখ্যা দুটিকে যোগ করুন, 7+5=12
তৃতীয় ধাপ,
যোগফলের প্রথম সংখ্যাকে (1) বসিয়ে দিন 7 এর মাথায় এবং ২ কে আগের নিয়মে যথা স্থানে রাখুন,
1
7 2 5
= 8 2 5 (যোগ করলে পাই)
এই হলো উত্তর: 825
প্রথম থেকে শেষ পর্যন্ত আর একবার পড়ুন, আপনি ৩ সেকেন্ডেই করতে পারবেন।
পর্ব -২
যোগ
বিয়োগ গুণ ভাগ নিয়ে আমরা অনেক সময় পেরেশান থাকি। ক্যালকুলেটরের অতি
ব্যবহারের ফলে আমরা অনেকেই সাধারণ যোগ বিয়োগ ভুলতে বসেছি। এই গণিত প্রয়োগ
করলে আমরা মুখে মুখে করতে পারি। আসুন দেখে নেই বিয়োগের কিছু
নিয়মকে……………।
ধরুন, আমরা 1000 থেকে 564 বিয়োগ দিতে
চাই। তাহলে আমরা একটি সূত্র অবলম্বন করবো। সুত্রটি মনে রাখলে আমরা খুব
সহজেই এটি কয়েক সেকেন্ডের মধ্য সমাধান করতে পারবো।
সূত্রটি হলো: সব সংখ্যাকে ৯ থেকে এবং শেষ সংখ্যাকে ১০ থেকে বিয়োগ দিতে হবে।
564 এর প্রতিটি সংখ্যাকে 9 থেকে এবং শেষ সংখ্যাকে 10 থেকে বিয়োগ দিলে আমরা উত্তর পাবো 436
লক্ষ্য করুন :

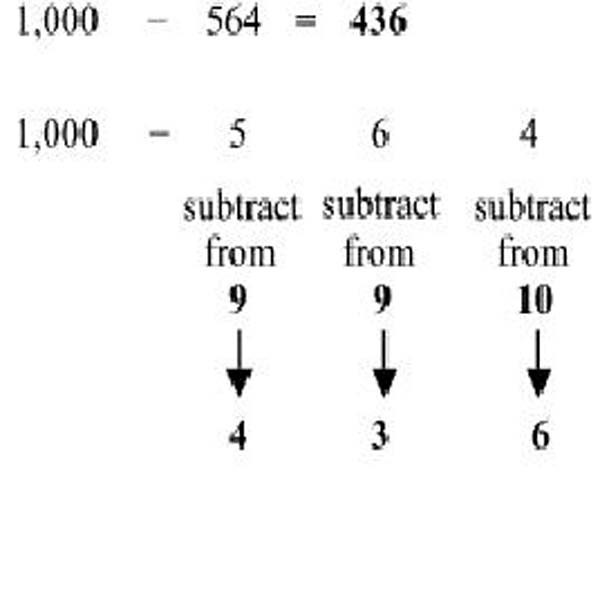
1000 – 564 =436
এখানে 9 থেকে প্রথমে 5 বিয়োগ দিন 9-5=4, আবার
9 থেকে 6 বিয়োগ দিন 9-6=3 , এবার
10 থেকে 4 বিয়োগ দিন 10-4=6
উত্তর হলো: 436
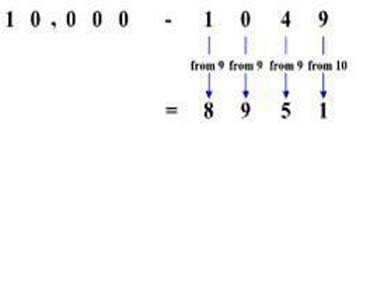
একই ভাবে,
10,000 – 1049 = 8951


আবার,
1000 – 83 এর বিয়োগের ক্ষেত্রে 83 কে 083 ধরে নিতে হবে।
সুতরাং 1000 – 83 হবে 1000 – 083 = 917
উত্তর হবে 917
মনে মনে মুখে মুখে করুন: (ঘড়ি ধরে সময় দেখুন)
1) 1000 – 289 =
2) 1000 – 797 =
3) 1000 – 505 =
4) 10000-4225 =
5) 10,000 – 8876 =
6) 10,000 – 1511 =
7) 100 – 37 =
8) 1000 – 89 =
9) 10,000 – 258 =
10) 10,000 – 29 =
[এখানে
এই গণিতের দুই একটি টেকনিক নিয়ে আলোচনা করা হয়েছে শুধুমাত্র ধারণা
দেয়ার জন্যে, আপনাদের ভালো লাগলে ভবিষ্যতে এই বিষয়ে আরও লেখার ইচ্ছা
রয়েছে]
মূল লিখাটা
এখানে
লেখক-
- এক বাঙালি ‘পরী’র হাতেই! ‘ফ্যাশনে’র মাছ!………….
- মরা গাঙে বান ডাকালেন ভারতীয় গবেষক, মঙ্গলে নদীর ফসি…
- বাংলায় বিজ্ঞানচর্চা ও সত্যেন্দ্রনাথ বসু …………
- ডাঃ কালী প্রদীপ চৌধুরীর না জানা ইতিহাস, বর্তমানে স…
- পৃথিবীর সর্বশ্রেষ্ঠ বেদবিদ ,ধর্মজ্ঞ ,মহাত্মা , জ্য…
- ইতিহাসের এক ভষ্কর অধ্যায় তৈমুর লং……………….
- বিজ্ঞানী নিউটনের পূর্বে বিজ্ঞানী ভাস্করাচার্য কি…
- আমাদের গণিত, গণিতের আমরা: মজার গণিতের সন্ধানে। লেখ.



